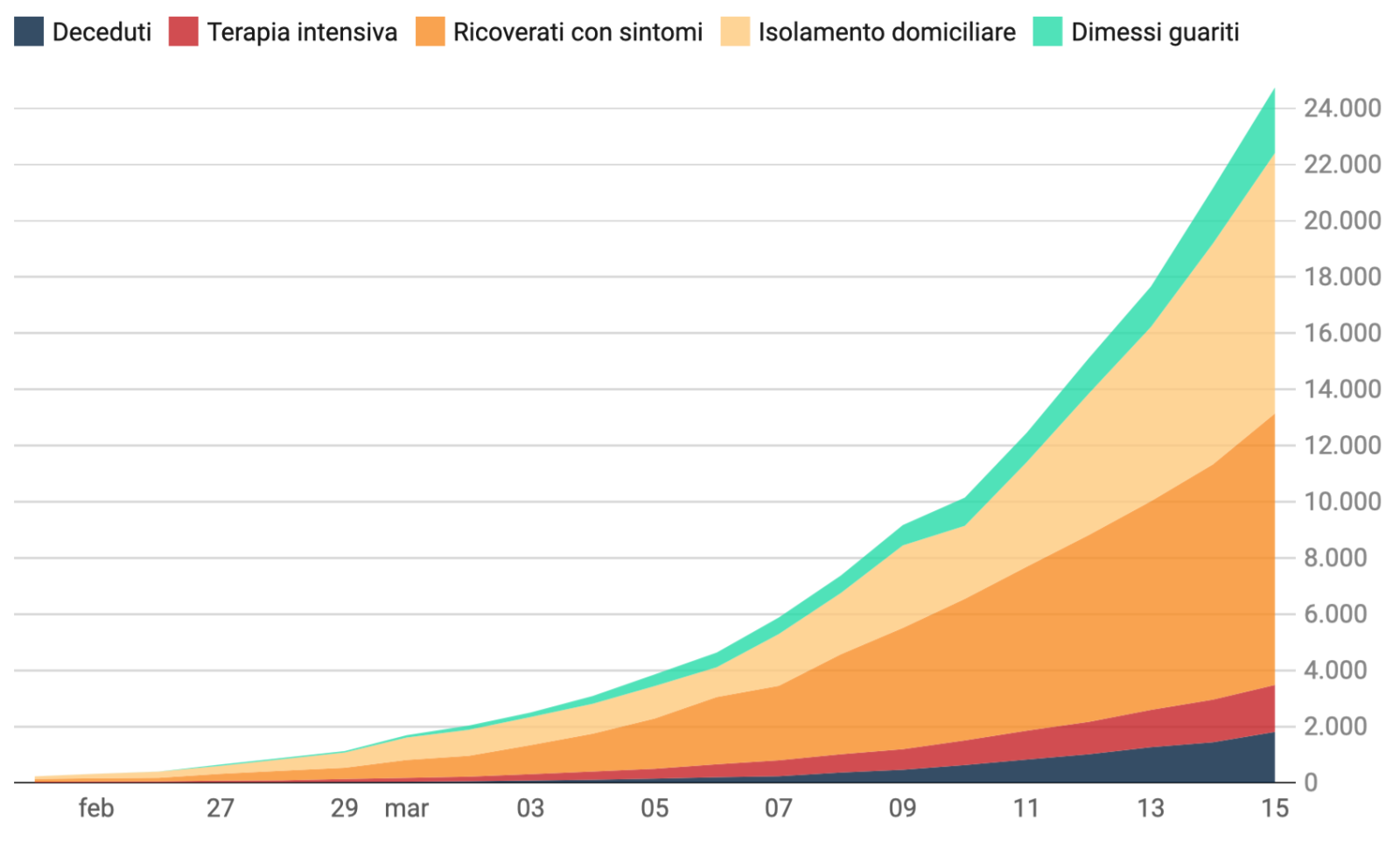
Presentiamo i risultati relativi all’analisi per la Lombardia, la Puglia e le sei province della Lombardia al momento maggiormente colpite, dei dati aggiornati alle 18 del 15 marzo 2020, che sostituiscono o integrano quelli nel documento del 14 Marzo. Vengono poi illustrati i risultati di un’analisi a livello nazionale su come l’epidemia si propaga all’interno del territorio italiano. I dati a livello regionale e nazionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github. com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 14-15 marzo la riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni 12-13 marzo e 13-14 marzo, come si può osservare in scala semi-logaritmica nella figura 1. Si spera che il trend si mantenga anche nei prossimi giorni.
Purtroppo, nelle regioni del centro-sud, ma più marcatamente in quelle del sud, persiste l’aumento del tasso di crescita della frazione dei contagiati osservati a partire dall’11 marzo dopo una precedente sua diminuzione, come già segnalato nel documento del 13 marzo e come si può vedere in figura 2 per la Puglia. Ribadiamo che la probabile principale causa di questo è l’esodo seguente il decreto che istituiva dall’8 marzo la zona rossa in Lombardia. Comportamenti come questo o come quello degli assalti ai supermercati prima che venissero introdotte delle modalità di accesso regolamentato sono da evitare perché inducono un aumento del rischio di contagio e di conseguenza contribuiscono alla diffusione dell’epidemia.
Per cinque delle sei province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano e Pavia, è presente, come nei giorni precedenti, la dimuzione del tasso di crescita, esclusa Pavia. Infatti per Pavia l’adattamento del modello geometrico (che non presenta riduzione del tasso di crescita) ai dati è molto buono (vedi figura 3).
Descriviamo ora i risultati di un’analisi sul modo in cui l’epidemia di coronavirus si sta diffondendo all’interno del territorio italiano. Sappiamo che l’epidemia in Italia è iniziata a Bergamo. Abbiamo quindi preso Bergamo come punto di riferimento per la diffusione dell’epidemia. Fissato un giorno qualsiasi, abbiamo considerato i dati del numero di contagiati osservati in ciascun capoluogo di provincia fino a quel giorno. Per ciascuna capoluogo, abbiamo calcolato la sua distanza da Bergamo. Come distanza abbiamo scelto la lunghezza del cammino più breve, lungo la superficie di una sfera col raggio pari a quello terrestre (6.371 km), tra i due punti corrispondenti al capoluogo ed a Bergamo. Per il giorno considerato abbiamo quindi per ogni capoluogo la sua distanza da Bergamo e il numero di contagiati osservati al suo interno fino a quel giorno. Possiamo quindi calcolare la “distanza media” da Bergamo per quel giorno dei punti (capoluoghi) dove sono stati registrati casi di coronavirus fino ad allora. La media è di tipo pesato con i pesi proporzionali al numero di casi registrati per ciascun capoluogo fino a quel giorno. Come usualmente fatto nello studio del fenomeno della diffusione classica di particelle, la distanza media è calcolata prendendo la radice quadrata della media pesata del quadrato della distanza citata. Osserviamo che questa analisi non si occupa di studiare la diffusione dell’epidemia lungo particolari direzioni, ma considera tutte le direzioni assieme. In figura 4 mostriamo come varia la distanza media considerata al variare del tempo. Dal grafico vediamo che, a parte delle fluttuazioni di nessun significato, questa distanza aumenta nel tempo, con il tasso di crescita che aumenta anch’esso fino ad un massimo, per poi diminuire, esattamente come si comporta teoricamente la frazione dei contagiati osservati. Abbiamo perciò effettuato un fit con un modello logistico e il risultato è sovrapposto ai valori calcolati per la distanza media. Notiamo che il valore massimo del tasso di crescita è raggiunto attorno al 9 marzo, il giorno dopo l’introduzione della zona rossa in Lombardia. Seppure potrebbe essere una coincidenza, ipotizziamo invece che ci sia una relazione causa effetto. Per ora il fenomeno dell’esodo non trova riscontro qui e questo può essere dovuto al modesto aumento di nuovi casi di contagiati osservati nelle regioni del sud in seguito all’esodo e soprattutto all’istituzione della zona rossa in tutto il paese.
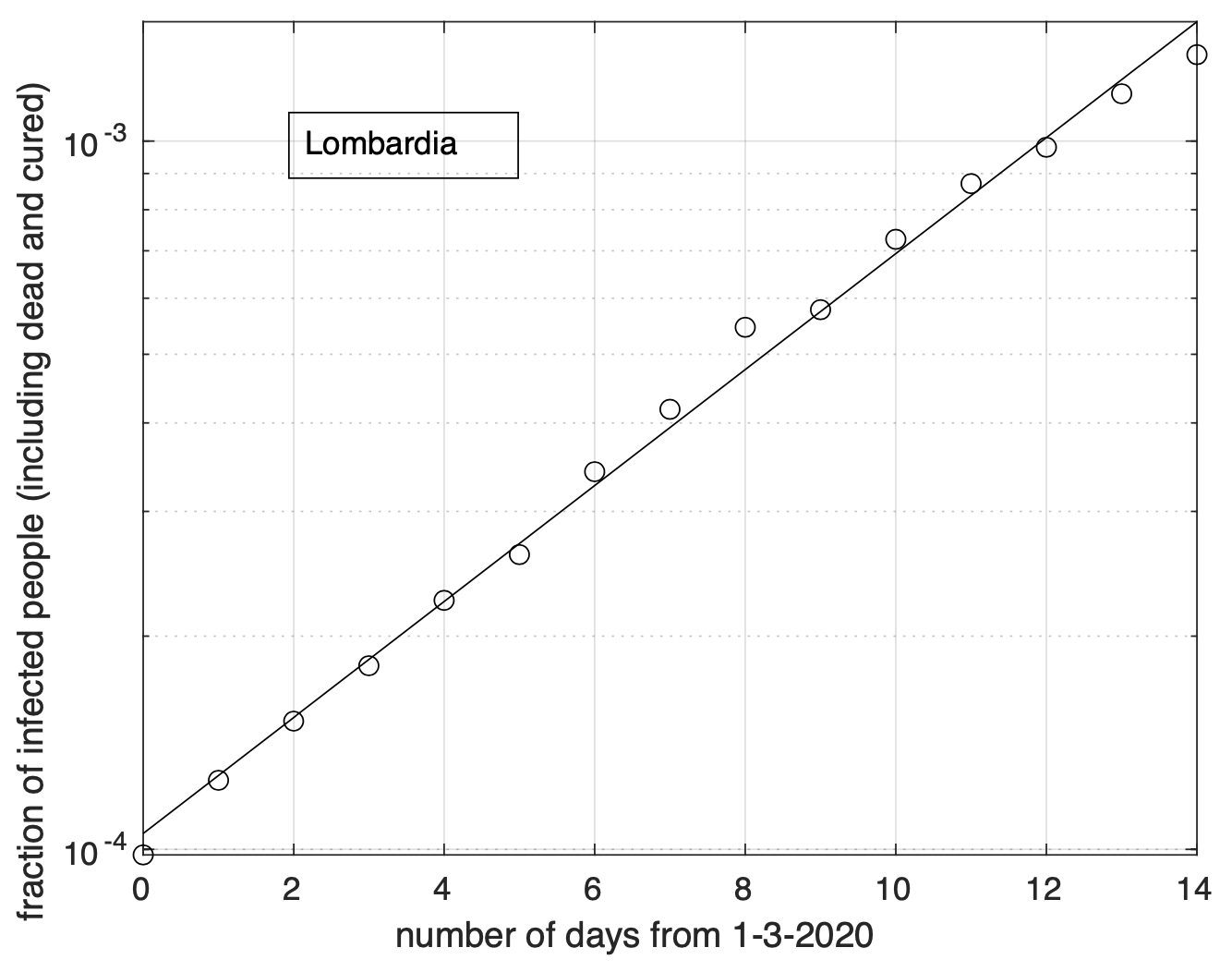
Figure 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 Marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello geometrico stimato a partire dai dati. Notiamo un buon adattamento del modello teorico ai dati e che gli ultimi tre punti sperimentali sono sotto la retta che corrisponde al miglior fit con un modello geometrico. Questo fornisce evidenza del trend di riduzione del tasso di crescita.
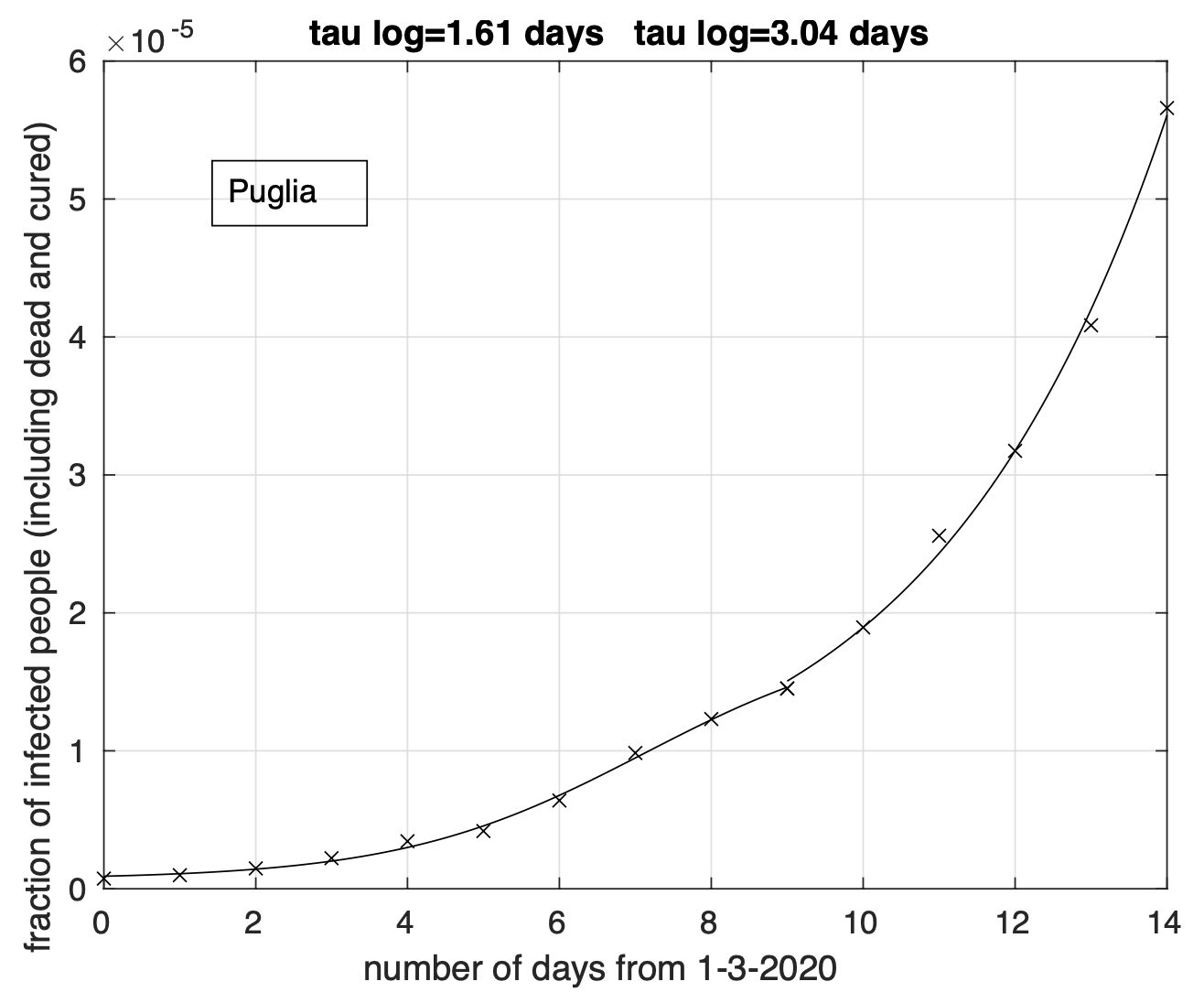
Figure 2. Frazione del numero di contagiati osservati in Puglia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
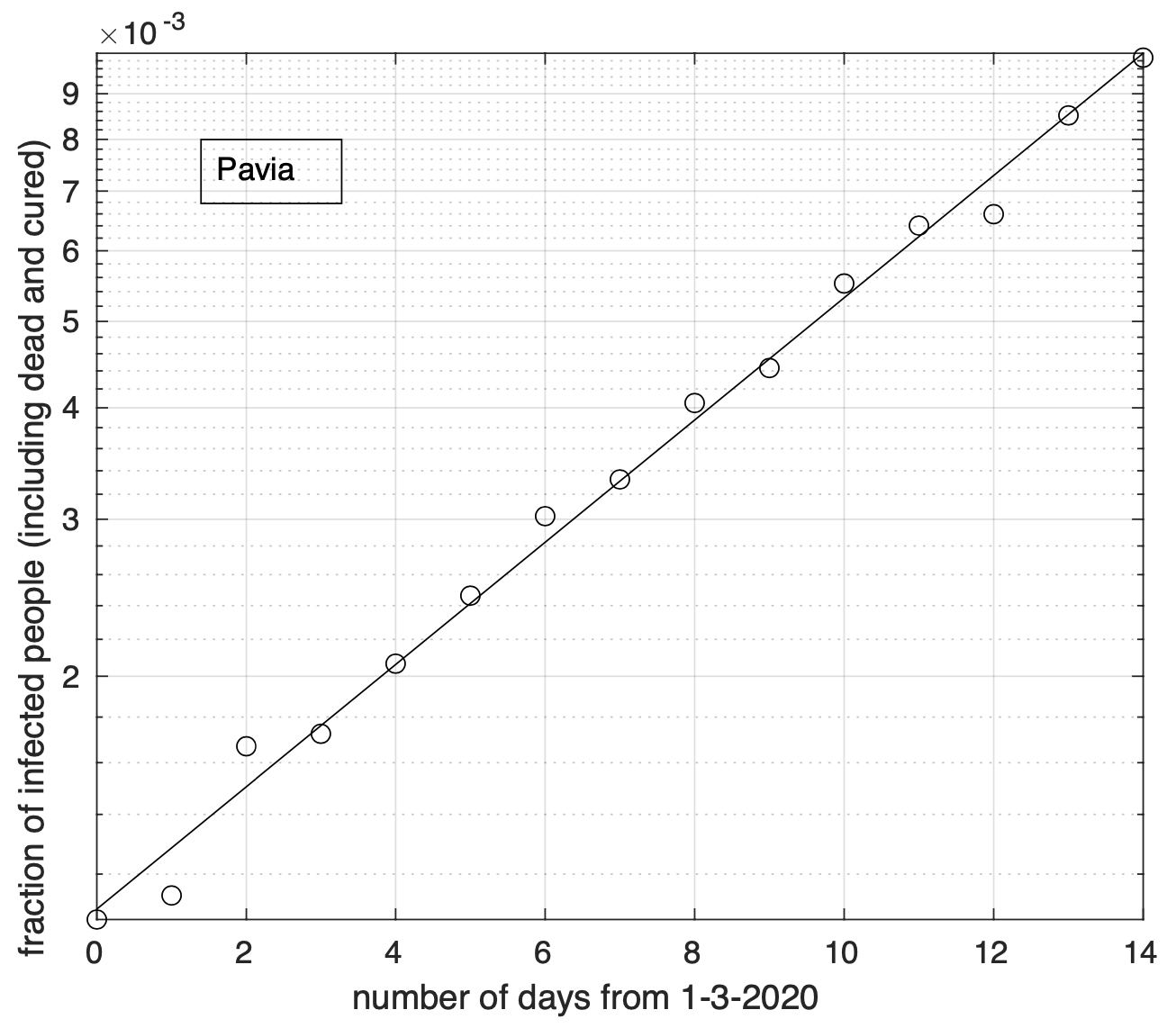
Figure 3. Sequenza temporale della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia (in scala semi-logaritmica). Il miglior fit con un modello geometrico è sovrapposto ai dati.
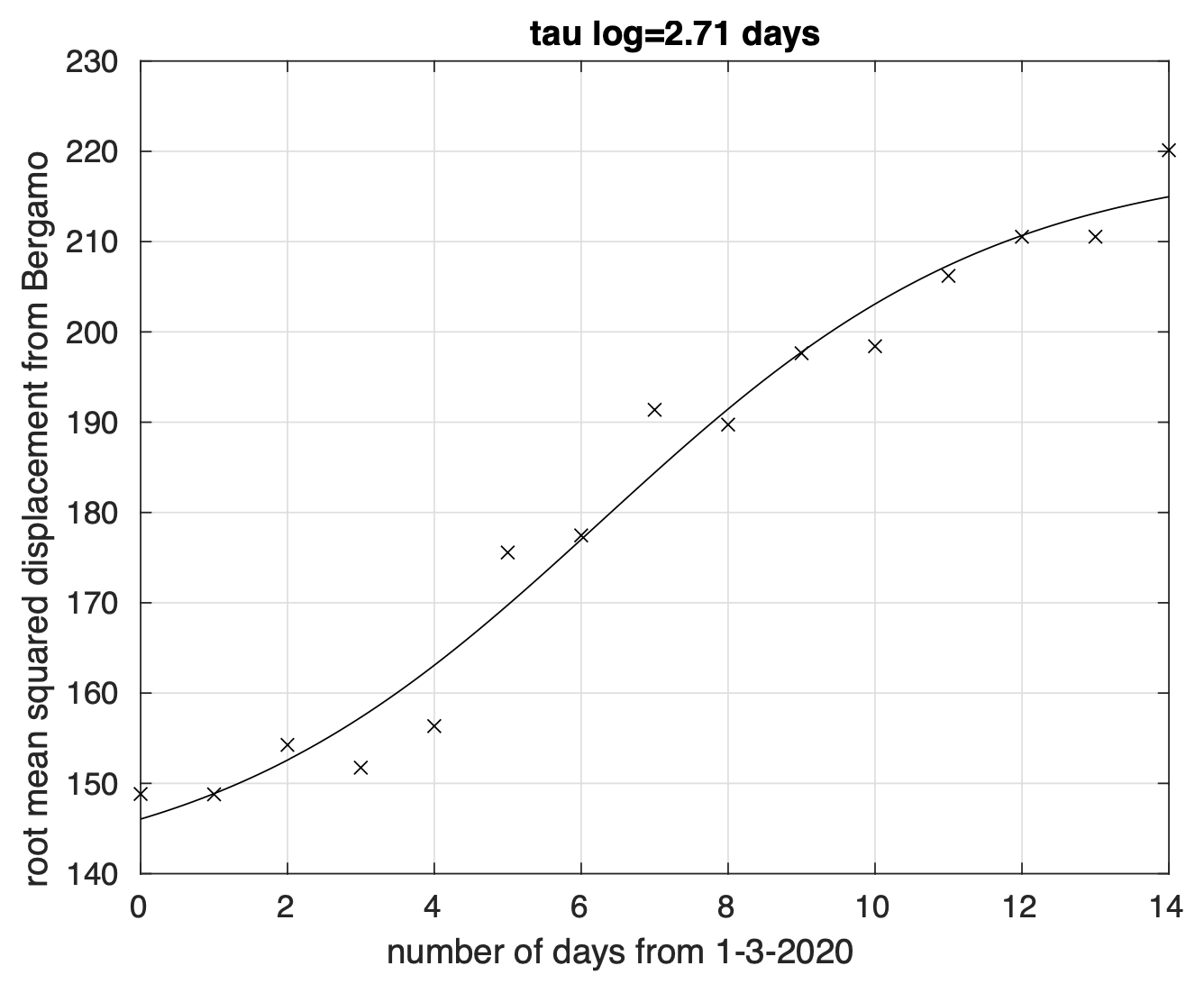
Figure 4. Andamento nel tempo della “distanza media” (in km) da Bergamo, origine della diffusione del coronavirus in Italia, dei punti del territorio italiano raggiunti dall’epidemia. Il miglior fit con un modello logistico è sovrapposto ai dati calcolati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
