
R(t) ormai è diventato come il PIL e come lo spread: un numero da cui dipendono molte, forse troppe cose. Visto che se ne parla tanto e che forse non tutti quelli che ne parlano sanno davvero di cosa si tratta, cerchiamo di capire meglio la questione.
Il processo di contagio prevede tre elementi: un individuo infetto, preso dalla popolazione che in un certo giorno è contagiosa, un individuo sano, preso dalla parte di popolazione che non ha contratto l’infezione ed un contatto sufficientemente prolungato e intenso tra i due individui da produrre un contagio.
Date condizioni stabili di una epidemia, condizioni in cui il contatto tra le persone per frequenza ed intensità medie non cambia nel tempo, il numero R0, chiamato numero di riproduzione di base determina il numero medio di contagi causati da una persona che, durante il periodo di infezione, risulti contagiosa. Quando R0 risulta minore di 1 l’epidemia si sta spegnendo, quando è maggiore di 1 sta espandendosi.
Se nel corso del tempo intervengono modifiche nelle modalità del distanziamento sociale, la velocità con cui l’epidemia si propaga cambia. In queste condizioni si usa un parametro dipendente dal tempo R(t) che viene via via aggiornato per rispecchiare le mutate condizioni del contagio.
Ma come si calcolano R0 e R(t) partendo dai dati a disposizione ?
Vi sono almeno 4 modi di effettuare questo calcolo: a) Bettencourt-Ribeiro-Systrom, b) Wallinga-Teunis c) una versione di (b) sviluppata dal Robert Koch Institute e d) una seconda versione di (b), EpiEstim, sviluppata dall’ Imperial College [1]. Quest’ ultima versione è considerata la più affidabile e precisa ed è quella usata anche dalla Fondazione Bruno Kessler [1][2] per calcolare i valori di R(t) per l’Istituto Superiore della Sanità, basandosi anche su dati sui flussi interregionali e internazionali non a disposizione del pubblico.
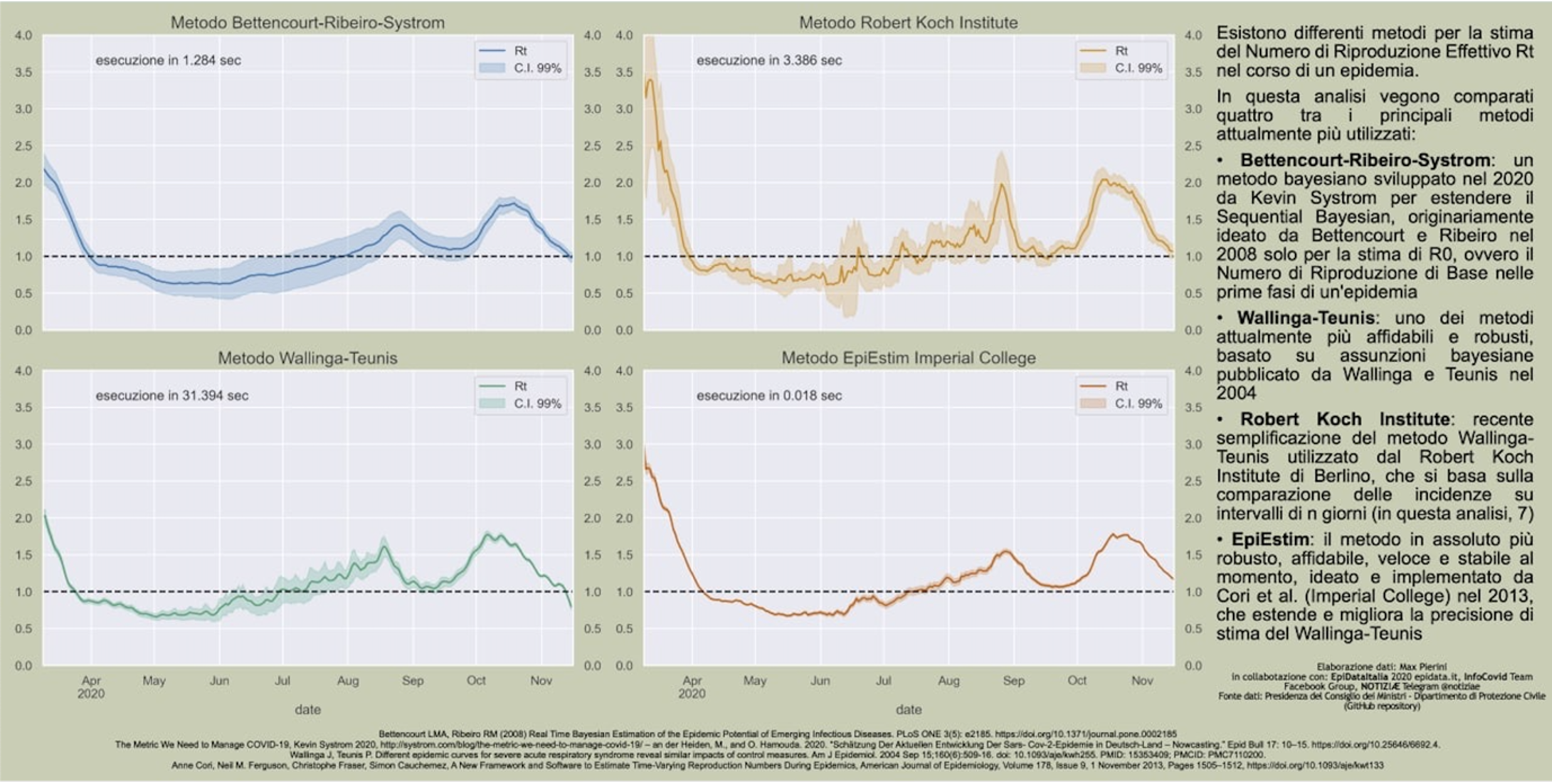
Fonte: https://www.epidata.it/Italia/stime_Rt.html
Questi metodi sono basati su una modellizzazione del contagio basato su distribuzioni statistiche che descrivono la probabilità di avere uno o più contatti e la durata del periodo di contagio.
Come si può vedere dalla figura 1, i quattro metodi applicati al periodo dell’ epidemia di Covid in Italia, danno risultati che mostrano differenze anche significative l’uno dall’ altro oltre ad avere diverse bande di incertezza. Questo rappresenta un problema quando il valore di R(t) viene usato come parametro soglia per determinare le restrizioni che caratterizzano il colore di una regione. L’algoritmo che viene usato per implementare questi metodi è piuttosto complicato e non è sostanzialmente possibile riprodurre esattamente i risultati che vengono resi periodicamente pubblici in quanto basati, almeno in parte, su dati non disponibili a tutti.
Nel seguito illustro una modalità operativa per calcolare R(t) che risulta molto semplice e che, soprattutto, è in grado di calcolare per definizione, una quantità che se risulta maggiore o minore di 1 corrisponde a un aumento o ad una diminuzione degli infetti attivi.
Una epidemia come quella del Covid-19 può essere descritta da un modello compartimentale di tipo SIR (Susceptible, Infected, Resolved), basato su un sistema di tre equazioni differenziali non lineari.
La prima di queste equazioni è la seguente (I(t) è il numero di infetti attivi, S(t) la popolazione ancora sana, N la popolazione totale):
d I(t)/dt = β r I(t) S(t)/N-γ I(t)
dove β è probabilità di trasmettere il contagio, r numero di contatti nell’unità di tempo e γ l’inverso del tempo di guarigione.
Se facciamo alcuni semplici passaggi, assumendo che S(t)/N sia un numero molto vicino a 1, otteniamo che:
(1/I(t) d I(t)/dt + γ)/γ = βr /γ = R0
Il termine 1/I(t) d I(t)/dt è la derivata di Ln(I(t)) e si può ricavare dai dati come coefficiente angolare della tangente a Ln (I(t)) presa su un intervallo di k-giorni , tipicamente k=7; γ è una costante, che risulta circa 1/9 giorni-1 e viene ricavata dai dati epidemici [2].
Usando la modellistica SIR si può quindi ricavare R*0 e il suo andamento R*(t), direttamente dai dati su I(t) con un procedimento molto semplice: per definizione, quando risulta d I(t)/dt = 0, la curva raggiunge il massimo e R*(t) = 1, come ci si aspetta dalla definizione di R. Ho chiamato questa quantità R* per distinguerle da quelle calcolate con gli algoritmi statistici.
E’ interessante confrontare R*(t) così ricavato con R(t) calcolato con EpiEstim, il metodo sviluppato dall’ Imperial College e usato dalla Fondazione Kessler e dall’ISS. La figura seguente mostra il confronto tra il metodo della derivata logaritmica ed il calcolo con EpiEstim nel corso dell’epidemia Covid-19: è interessante notare il buon accordo tra i due metodi, che nella maggior parte concordano entro 0,1 unità, in particolare nella fase attuale tra settembre e novembre.
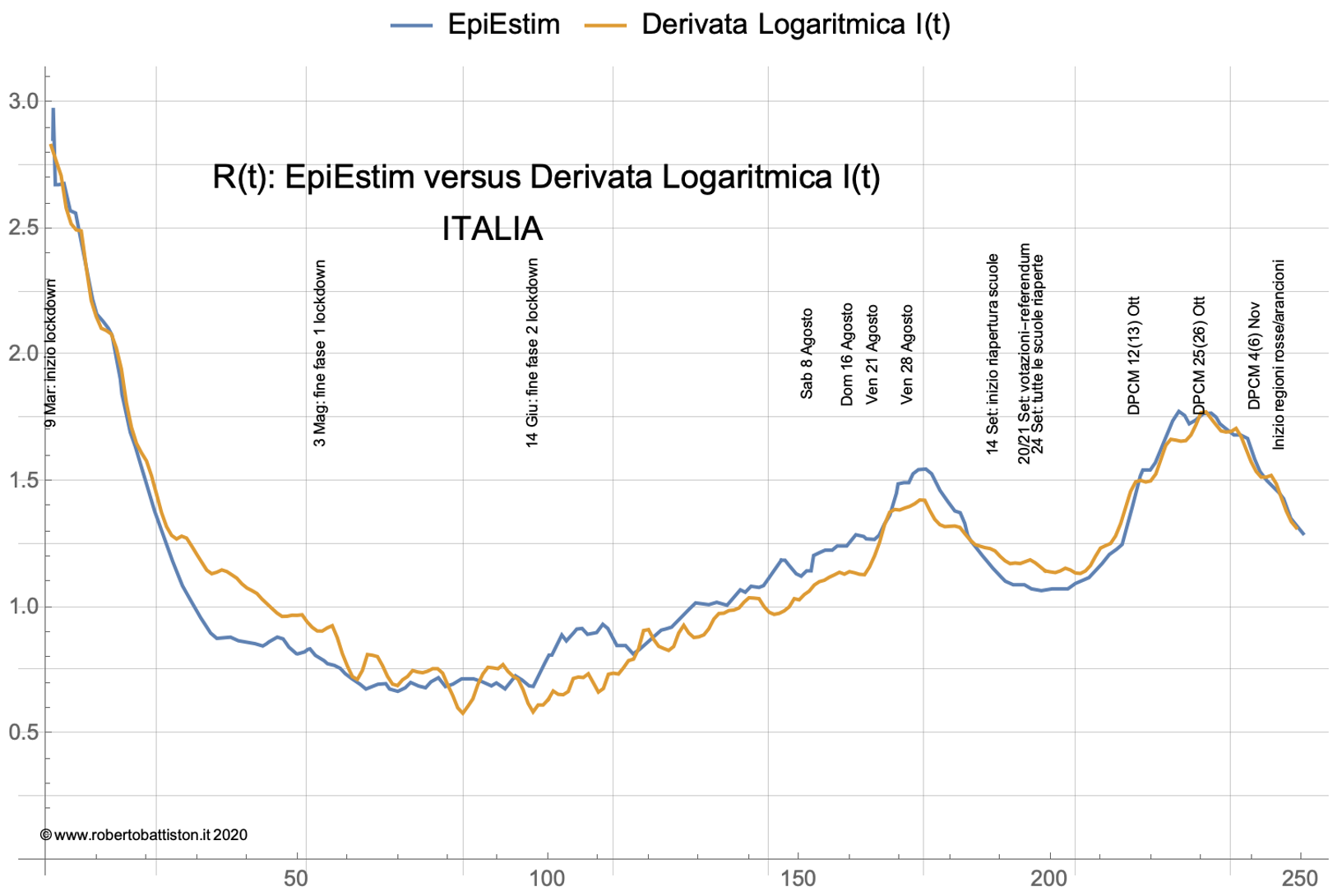
Usando il metodo della derivata logaritmica possiamo descrivere in modo coerente l’andamento di I(t) nel corso degli ultimi mesi in funzione di R*(t): risulta anche piuttosto semplice estrapolare l’andamento di I(t) assumendo che la tendenza alla decrescita di R*(t) continui nelle prossime settimane. Essendo R*(t) ricavato direttamente dai dati non è affetto dalla significativa forchetta di errore come nel caso in cui venga determinato usando un modello probabilistico.
Considerata la dispersione che si ottiene nel calcolo di R(t) con i vari metodi statistici e l’importanza di avere un algoritmo condiviso, si potrebbe considerare di usare R*(t), fermo restando che è necessario approfondire l’errore sistematico indotto dal semplice algoritmo utilizzato: la coerenza con il calcolo EpiEstim suggerisce però che questo errore non dovrebbe essere grande.
Questo modo empirico di calcolare di R(t) risulta infatti trasparente, rapido e auto-consistente permettendo di determinare l’andamento nel tempo di un parametro fondamentale per capire l’andamento dell’ epidemia, sia in Italia che nelle singole regioni, come illustrato nella seguente figura.
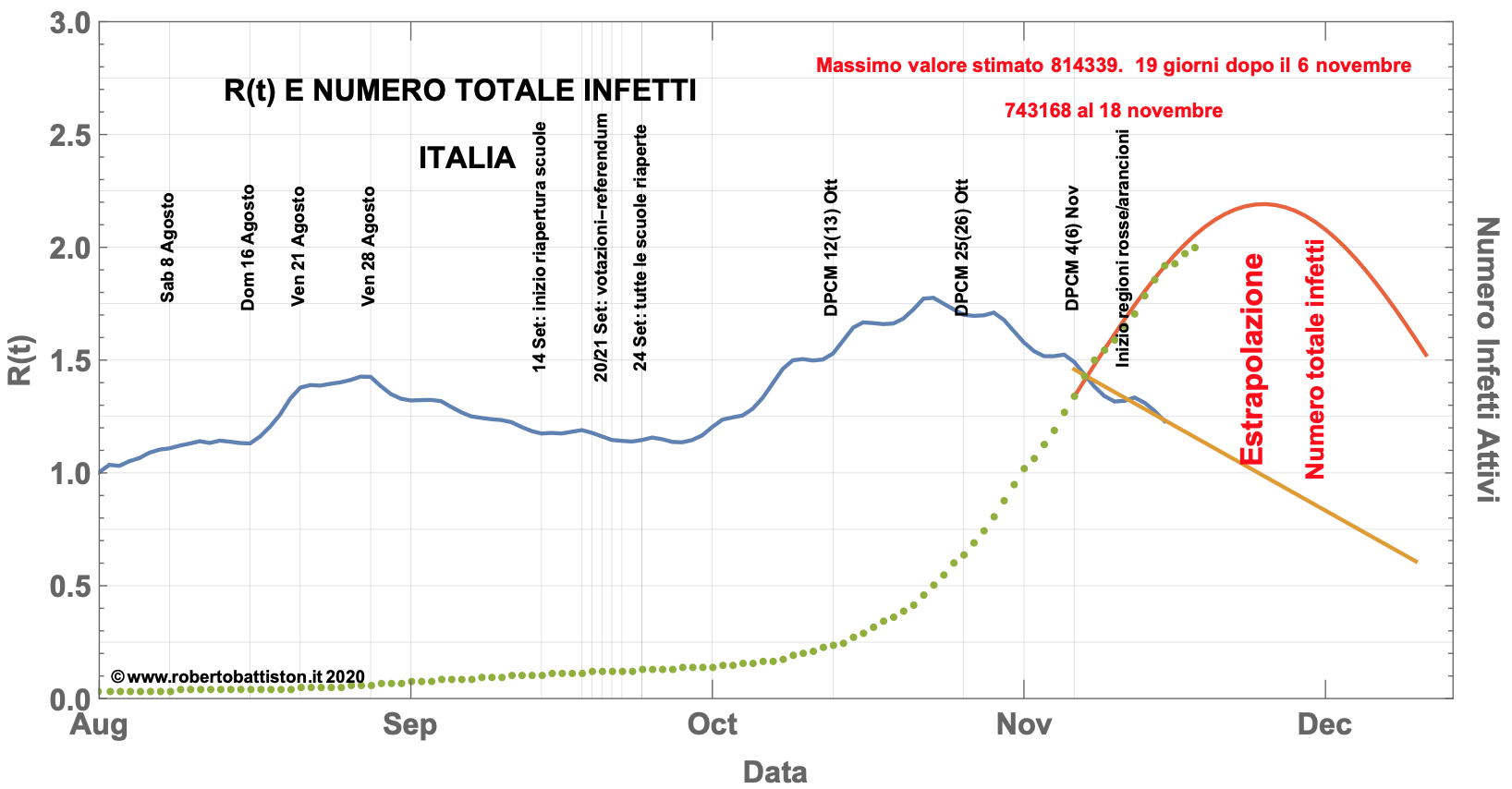
Fonte: https://www.robertobattiston.it
Note
[1] Cori A, Ferguson NM, Fraser C, Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. 2013;178(9):1505-1512. doi:10.1093/aje/kwt133
[2] D Cereda, M Tirani, F Rovida, V Demicheli, M Ajelli, P Poletti, F Trentini, G Guzzetta, V Marziano, A Barone, M Magoni, S Deandrea, G Diurno, M Lombardo, M Faccini, A Pan, R Bruno, E Pariani, G Grasselli, A Piatti, M Gramegna, F Baldanti, A Melegaro, S Merler. The early phase of the COVID-19 outbreak in Lombardy, Italy. ArXiv:2003.09320v1, 2020.

